Chúng tôi rất vui mừng chia sẻ kiến thức sâu sắc về từ khóa Permutation la gi để tối ưu hóa nội dung trang web và tiếp thị trực tuyến. Bài viết cung cấp phương pháp tìm kiếm, phân tích từ khóa và chiến lược hiệu quả. Cảm ơn sự quan tâm và hãy tiếp tục theo dõi để cập nhật kiến thức mới.
Các tham khảo thêm:
Bạn Đang Xem: Permutation và Combinations
- Các hình vẽ cơ bản trong AI
- Các nguyên tắc đếm cơ bản
- Phân khối khóa (key) trong mã hóa
- Các chức năng vẽ của OpenCv
- Function trong toán học
Permutation:
Bất kỳ sự sắp xếp nào của một tập hợp n đối tượng người dùng theo một trật tự nhất định được gọi là Permutation của Đối tượng người tiêu dùng. Mọi sự sắp xếp bất kỳ r ≤ n của đa số đối tượng người dùng này theo một trật tự nhất định được gọi là một Permutation r hoặc một Permutation của n đối tượng người dùng được lấy r tại một thời khắc.
Nó được ký hiệu là P (n, r)
Định lý: Chứng minh rằng số Permutation của n vật được thực ngày nay một thời khắc là n !.
Chứng cớ: Chúng tôi biết rằng
Ví dụ:
Lời giải:

Permutation có hạn chế:
Số lần Permutation của n đối tượng người dùng khác nhau được thực hiện r tại một thời khắc mà p đối tượng người dùng cụ thể không xẩy ra là
Số lần Permutation của n đối tượng người dùng khác nhau được thực hiện r tại một thời khắc mà p đối tượng người dùng cụ thể có mặt là
Ví dụ: Có thể lập bao nhiêu số có 6 chữ số bằng phương pháp dùng các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8 nếu mọi số khai mạc bằng ’30’ không có chữ số nào được tái diễn?
Lời giải: Tất cả những số khai mạc bằng ’30. Do đó, tất cả chúng ta phải chọn 4 chữ số từ 7 chữ số còn sót lại.
Xem Thêm : Thương lái là gì? Vai trò của thương lái trong hoạt động kinh doanh
∴ Tổng số các số khai mạc bằng ’30’ là
Permutation với những đối tượng người dùng tái diễn:
Định lý: Chứng minh rằng số các Permutation khác nhau của n đối tượng người dùng phân biệt được thực ngày nay một thời khắc mà mọi đối tượng người dùng được phép tái diễn một số lần bất kỳ là nr.
Chứng minh: Giả sử rằng với n đối tượng người dùng, tất cả chúng ta phải điền vào r vị trí khi được cho phép tái diễn đối tượng người dùng.
Do đó, số cách điền vào vị trí thứ nhất là = n
Số cách điền vào vị trí thứ hai = n
………………………..
………………………..
Số cách điền vào vị trí thứ r = n
Như vậy, tổng số cách điền r chỗ có n thành phần là
= n. N. n ………….. r lần = nr.
Permutation tròn:
Một Permutation được thực hiện xung quanh một vòng tròn được gọi là Permutation tròn.

Ví dụ: Có bao nhiêu cách xếp các vần âm a, b, c, d, e, f, g, h, i, j thành một hình tròn?
Xem Thêm : Lệnh ATC là gì trong chứng khoán? Đặc điểm và ví dụ cụ thể về lệnh ATC
Bài giải: (10 – 1) = 9! = 362880
Định lý: Chứng minh rằng số Permutation đường tròn của n vật thể khác nhau là (n-1)!
Chứng minh: Ta coi K là số Permutation cấp thiết.
Với mỗi Permutation vòng như vậy của K thì có n Permutation tuyến tính tương ứng. Như đã trình bày trước đó, tất cả chúng ta khởi đầu từ mọi đối tượng người dùng của n đối tượng người dùng trong các Permutation vòng tròn. Như vậy, với K Permutation vòng, ta có K … n Permutation tuyến tính.

Combination
Combinations là việc lựa chọn một số hoặc tất cả những đối tượng người dùng từ một tập hợp các đối tượng người dùng nhất định, trong đó trật tự của đa số đối tượng người dùng không quan trọng. Số lượng Combinations của n đối tượng người dùng, lấy r tại một thời khắc được biểu thị bằng nCr hoặc C (n, r).
Chứng minh: Số Permutation của n thứ khác nhau, lấy r tại một thời khắc được cho bởi
Vì không có vấn đề gì về trật tự sắp xếp của đa số đối tượng người dùng, do đó, với mọi sự Combinations của r vật, đều sở hữu r! sắp xếp tức là,
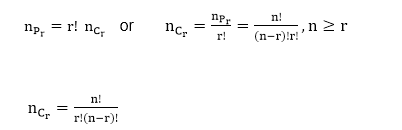
Ví dụ: Một người nông dân mua 3 con bò, 2 con lợn và 4 con gà mái từ một người nam giới có 6 con bò, 5 con lợn và 8 con gà mái. Tìm số m cách chọn mà người nông dân có.
Người nông dân có thể chọn bò Theo phong cách C (6, 3), lợn Theo phong cách C (5, 2) và gà mái Theo phong cách C (8, 4). Do đó số m cách chọn như sau:
Xem thêm Mã hóa ELGAMAL
Một số thắc mắc phổ quát về permutation và combinations
- Permutation và combinations là gì? Permutation và combinations là hai khái niệm trong toán học để đếm số cách sắp xếp hoặc lựa chọn ra các thành phần từ một tập hợp cho trước.
- Permutation là gì? Permutation là số cách sắp xếp các thành phần của một tập hợp theo một trật tự nào đó. Số permutation của một tập hợp n thành phần là n! (n giai thừa).
- Combinations là gì? Combinations là số cách lựa chọn ra k thành phần từ một tập hợp n thành phần mà không quan tâm đến trật tự. Số combinations của một tập hợp n thành phần và k thành phần được tính bằng công thức C(n, k) = n!/[(n-k)!k!].
- Công thức chung để tính số permutation và combinations là gì?
- Số permutation của n thành phần được tính bằng n!.
- Số combinations của n thành phần và k thành phần được tính bằng C(n, k) = n!/[(n-k)!k!].
- Permutation và combinations khác nhau thế nào?
- Permutation liên quan tới việc sắp xếp các thành phần trong một tập hợp, trong những lúc combinations liên quan tới việc lựa chọn các thành phần trong một tập hợp mà không quan tâm đến trật tự.
- Số permutation của một tập hợp n thành phần là n!, trong những lúc số combinations của một tập hợp n thành phần và k thành phần được tính bằng công thức C(n, k) = n!/[(n-k)!k!].
- Trong Python, có thư viện nào tương trợ tính số permutation và combinations không? Trong Python, thư viện math tương trợ tính số permutation và combinations thông qua các hàm math.perm() và math.comb().
- Hàm math.perm() trong Python là gì? Hàm math.perm(n, k) trong Python trả về số permutation của n thành phần và k thành phần. Nó được tính bằng công thức n!/(n-k)!.
Ví dụ:
- Hàm math.comb() trong Python là gì? Hàm math.comb(n, k) trong Python trả về số combinations của n thành phần và k thành phần. Nó được tính bằng công thức n!/(n-k)!k!.
Ví dụ:
- Làm thế nào để tính số permutation hoặc combinations trong Python nếu không sử dụng thư viện math? Nếu không sử dụng thư viện math, ta có thể sử dụng hàm đệ quy để tính số permutation hoặc combinations. Ví dụ:


