Chúng tôi rất vui mừng chia sẻ kiến thức về từ khóa Vecto la gi để tối ưu hóa nội dung trang web và tiếp thị trực tuyến. Bài viết cung cấp phương pháp tìm kiếm, phân tích từ khóa và chiến lược hiệu quả. Cảm ơn sự quan tâm và hãy tiếp tục theo dõi để cập nhật kiến thức mới.
Có thể bạn quan tâm
Khi đối chiếu với học trò lớp 10, vectơ là một khái niệm hoàn toàn mới mẻ vì vậy ở nội dung bài viết này tất cả chúng ta sẽ cùng thầy Lưu Huy Thưởng (giáo viên môn Toán tại Khối hệ thống giáo dục & đào tạo HOCMAI )cùng tìm hiểu về vectơ.
Bạn Đang Xem: Vectơ là gì? Các định nghĩa về vectơ – Môn Toán – Lớp 10
Mục lục
1. Khái niệm vectơ2. Hai Vectơ cùng phương3. Vectơ cùng hướng – vectơ bằng nhau4. Vectơ- không
1. Khái niệm vectơ
Cho hai điểm phân biệt A và B gọi là đoạn thẳng AB (có thể gọi là đoạn thẳng BA) không có sự khác nhau về thực chất. (ví dụ: ảnh dưới)
Trong thực tế, với 2 vị trí khác nhau, tất cả chúng ta cần chiều đi của nó. Ví dụ: chiều TP. Hà Nội vào TP.TP.Hồ Chí Minh sẽ khác chiều đi từ TP.TP.Hồ Chí Minh ra TP. Hà Nội. Vì vậy, trong toán học, để trình diễn chiều đi của nó: Chiều đi từ A tới B hoặc từ B tới A, người ta sẽ có được khái niệm vectơ ra đời. Cụ thể như sau:
- Chiều đi từ A tới B (ví dụ: ảnh dưới)Ta có vectơ AB, trong đó A là điều đầu, B là điều cuối.
- Chiều đi từ B tới A (ví dụ: ảnh dưới)
Ta có vecto BA, trong đó B được gọi là điều đầu, A được gọi là điều cuối
Như vậy, cho hai điểm phân biệt A và B để trình diễn chiều đi của đoạn thẳng AB ta sử dụng vectơ AB. 
=> Khái niệm vectơ: Vectơ là một đoạn thẳng được bố trí theo hướng.
Xem Thêm : Giải mã ý nghĩa I Love You 3000 là gì? Câu nói có gì thú vị?
Kí hiệu: Người ta sẽ dùng điểm đầu và điểm cuối của véc tơ để thể hiện vectơ bằng chữ in hoa, ngoài ra có thể sử dụng chữ in thường
Ví dụ: 
2. Hai Vectơ cùng phương
Với đoạn thẳng AB ta sẽ dựng đường thẳng AB, với 2 điểm A và B ta có hai vectơ AB và BA thì ta thấy rằng vectơ AB nằm toàn bộ trên tuyến đường thẳng AB thì kho đó ta nói rằng đường thẳng AB là giá của vectơ AB.
=> Giá của vectơ là một đường thẳng chứa vectơ đó.
Cho 2 đường thẳng d1 và d2 song song với nhau, với những điểm A,B,C,D,E,F (như hình) ta xét vectơ AB, vectơ BC, vectơ ED, vectơ EF.
Vectơ AB, vectơ BC có mức giá là d1 là các vectơ cùng phương với nhau.
Vectơ ED, vectơ EF có mức giá là d2 là các vectơ cùng phương với nhau.
=> Hai vectơ cùng phương là hai vectơ có mức giá song song hoặc trùng nhau
Ví dụ: 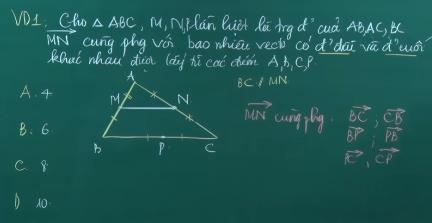
3. Vectơ cùng hướng – vectơ bằng nhau
Xem Thêm : HỌC LẬP TRÌNH PLC TRÊN MÁY MÓC THỰC TẾ
a, Vectơ cùng hướng: Là hai vectơ cùng phương và có chiều giống nhau
Xét hình bình hành ABCD tìm véc tơ cùng phương với vectơ AB được lấy từ 4 điểm ABCD thỏa mãn điểm đầu và điểm cuối khác nhau. 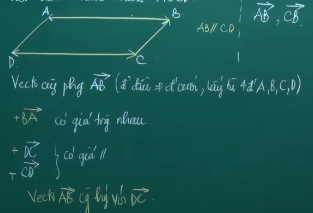
Ta thấy rằng vectơ AB cùng hướng từ trái sang phải với vectơ DC nên đây là hai vectơ cùng hương với nhau.
Lưu ý: Hai vectơ cùng phương thì có thể cùng hướng hoặc ngược hướng.
Từ đó ta có Tóm lại trong việc chứng minh 3 điểm thẳng hàng. Ta có 3 điểm phân biệt A, B,C để chứng minh 3 điểm này thẳng hàng ta sẽ xét tính cùng phương của vectơ AB và AC hoặc AB và BC. Nếu 2 vectơ này cùng phương thì suy ra 3 điểm A,B,C thẳng hàng và trái lại.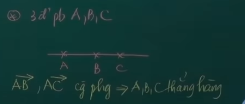 b,Vectơ bằng nhau: Là hai vectơ cùng hướng và cùng độ dài
b,Vectơ bằng nhau: Là hai vectơ cùng hướng và cùng độ dài
Ta có vectơ AB có điểm đầu là A điểm cuối là B thì độ dài vectơ AB đấy là độ dài của đoạn thẳng AB.
Độ dài của vectơ là khoảng tầm cách giữa điểm đầu và điểm cuối của nó.
Xét hình bình hành ABCD ta có AB=DC, AB//DC và cùng hướng với nhau nên vectơ AB bằng vectơ CD.
Trong mặt phẳng cho trước một vectơ và một điểm nhất quyết bất kì ta sẽ xác định được một điểm sao cho vectơ có điểm đầu cho trước và vectơ vừa cho là hai vectơ bằng nhau.
Ví dụ: 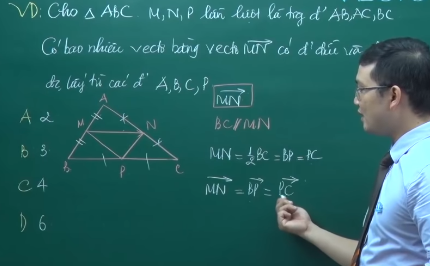 4. Vectơ- không Là vectơ là vectơ có điểm đầu và điểm cuối trùng nhau Tính chất:
4. Vectơ- không Là vectơ là vectơ có điểm đầu và điểm cuối trùng nhau Tính chất:
- Vectơ không cùng phương và cung hướng với mọi vectơ
- Mọi vectơ không đều bằng nhau
- Độ dài của vectơ không xoành xoạch bằng không
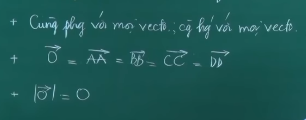
Hy vọng với nội dung bài viết kèm video giảng dạy của thầy Lưu Huy Thưởng về vectơ sẽ giúp ích cho những em trong quá trình nhập môn đại số 10.


