Chúng tôi rất vui mừng chia sẻ kiến thức sâu sắc về từ khóa Tu dien deu la gi để tối ưu hóa nội dung trang web và tiếp thị trực tuyến. Bài viết cung cấp phương pháp tìm kiếm, phân tích từ khóa và chiến lược hiệu quả. Cảm ơn sự quan tâm và hãy tiếp tục theo dõi để cập nhật kiến thức mới.
VnDoc xin mời các bạn cùng tham khảo tài liệu Tứ diện đều được VnDoc.com tổng hợp và soạn. Mời thầy cô và các bạn học trò cùng theo dõi nội dung bài viết tại chỗ này.
Bạn Đang Xem: Tứ diện đều
1. Tứ diện
- Tứ diện là hình có bốn đỉnh, thường được kí hiệu A, B, C, D. Bất kì điểm nào trong số những điểm trên được gọi là đỉnh, mặt tam giác đối diện với đỉnh này được gọi là đáy.
- Ví dụ: Chọn A là đỉnh thì (BCD) là mặt đáy.
2. Tứ diện đều
- Tứ diện đều là tứ diện có 4 mặt là tam giác đều.
- Tứ diện đều là một hình chóp tam giác đều.
- Hình chóp tam giác đều phải sở hữu thêm tham gia cạnh bên bằng cạnh đáy là tứ diện đều.
3. Tính chất tứ diện đều
– Tứ diện đều có những tính chất như sau:
+ Bốn mặt xung quanh là các tam giác đều bằng nhau.+ Các mặt của tứ diện là những tam giác có ba góc đều nhọn.+ Tổng các góc tại một đỉnh bất kì của tứ diện là 180.
+ Hai cặp cạnh đối diện trong một tứ diện có độ dài bằng nhau.+ Tất cả những mặt của tứ diện đều tương đương nhau.+ Bốn đường cao của tứ diện đều phải sở hữu độ dài bằng nhau.+ Tâm của khá nhiều mặt cầu nội tiếp và ngoại tiếp nhau, trùng với tâm của tứ diện.+ Hình hộp ngoại tiếp tứ diện là hình hộp chữ nhật.+ Các góc phẳng nhị diện ứng với mỗi cặp cạnh đối diện của tứ diện bằng nhau.+ Đoạn thẳng nối trung điểm của khá nhiều cạnh đối diện là một đường thẳng đứng vuông góc của tất cả hai cạnh đó.+ Một tứ diện có ba trục đối xứng.+ Tổng các cos của khá nhiều góc phẳng nhị diện chứa cùng một mặt của tứ diện bằng 1.
4. Cách vẽ tứ diện đều
Bước 1: Trước nhất các bạn hãy xem hình tứ diện đều là môt hình chóp tam giác đều ABCD.Bước 2: Tiến hành vẽ mặt là cạnh đáy ví dụ là mặt BCD.Bước 3: Tiếp theo những bạn tiến hành vẽ một đường trung tuyến của mặt đáy BCD. Ví dụ đường trung tuyến này là BM.Bước 4: Sau đó các bạn tiến hành xác định trọng tâm G của tam giác BCD nàyBước 5: Tiến hành dựng đường cao.Bước 6: Xác định điểm A trên tuyến đường vừa dựng và hoàn thiện hình tứ diện đều.
5. Thể tích tứ diện đều
– Một tứ diện đều sẽ có được 6 cạnh bằng nhau và 4 mặt tam giác đều sẽ có những công thức tính thể tích như sau:
+ Thể tích tứ diện ABCD: Thể tích của một khối tứ diện bằng một phần ba tích số của diện tích S mặt đáy và độ cao của khối tứ diện tương ứng:  + Thể tích tứ diện đều tam giác S.ABC: Thể tích của một khối chóp bằng một phần ba tích số của diện tích S mặt đáy và độ cao của khối chóp đó:
+ Thể tích tứ diện đều tam giác S.ABC: Thể tích của một khối chóp bằng một phần ba tích số của diện tích S mặt đáy và độ cao của khối chóp đó: 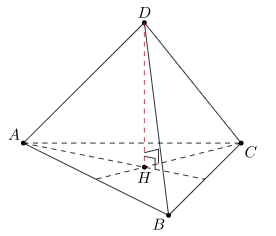
6. Công thức tính nhanh thể tích tứ diện đều cạnh a
Cho tứ diện đều ABCD cạnh a. từ A kẻ AH là đường cao của hình chóp A.BCD, H thuộc (BCD) thì H sẽ là tâm của tam giác đều BCD. Suy ra
- Độ cao của hình chóp A.BCD đều cạnh a là
- Thể tích khối tứ diện đều cạnh a là
4. Bài tập tính thể tích khối tứ diện đều
Câu 1: Khối chóp tứ diện đều cạnh a có thể tích bằng:
Câu 2: Số mặt phẳng đối xứng của hình tứ diện đều là:
A. 4 mặt phẳngB. 6 mặt phẳngC. 8 mặt phẳngD. 10 mặt phẳng
Câu 3: Trung điểm các cạnh của một tứ diện đều tạo thành:
A. Các đỉnh của một hình hai mươi mặt đều.
B. Các đỉnh của một hình mười hai mặt đều.
Xem Thêm : Insider Release Preview Là Gì, Cách Tham Gia Window Insider Là Gì, Windows
C. Các đỉnh của một hình bát diện đều.
D. Các đỉnh của một hình tứ diện.
Câu 4: Cho khối chóp tam giác đều S. ABC có cạnh đáy bằng a, cạnh bên gấp gấp hai cạnh đáy. Tính theo a thể tích V của khối chóp S.ABC.
Câu 5: Cho hình chóp tam giác đều S.ABC có cạnh đáy a và cạnh bên bằng . Tính thể tích khối chóp S.ABC.
Câu 6: Cho tứ diện đều ABCD có thể tích bằng 12 và G là trọng tâm của tam giác BCD. tính thể tích của khối chóp A.GBC.
Câu 7: Cho tứ diện đều ABCD có canh 2a. Tính thể tích khối tứ diện ABCD theo a
Câu 8: Cho tứ diện đều ABCD có canh . Tính thể tích khối tứ diện ABCD theo a
Câu 9: Cho tứ diện đều ABCD có thể tích bằng 1. Tìm độ dài các cạnh của tứ diện
A.
B.
C.
D.
Bài tập tự luận
Bài 1: Hãy tính thể tích khối tứ diện đều ABCD biết:
a) cạnh AB = 4 cm
b) cạnh CD = 6 cm
Xem Thêm : Adobe Encore
c) cạnh BD = 3 cm
Hướng dẫn giải
a) Vì là tứ diện đều nên các cạnh có độ dài bằng nhau: BC = CD = DA = BD = AC = AB = 4 cm nên thể tích là
Cho hình tứ diện đều ABCD cạnh a = 5 cm. Hỏi thế tích bằng bao nhiêub) Vì là tứ diện đều nên AB = BC = DA = BD = AC = CD = 6 cm nên thể tích là
c) Vì là tứ diện đều nên AB = BC = CD = DA = AC = BD = 3 cm nên thể tích
Bài 2: Cho hình chóp đều S.ABCD (đáy là hình vuông), đường SA vuông góc với mặt phẳng (ABCD). Xác định hình chóp này còn có mặt đối xứng nào.
Lời giải:
Ta có: BD vuông góc với AC, BD vuông góc với SA. Suy ra, BD vuông góc với (SAC). Từ đó ta suy ra (SAC) là mặt phẳng trung trực của BD. Ta tóm lại rằng, (SAC) là mặt đối xứng của hình chóp và đây là mặt phẳng duy nhất.
Bài 3: Tìm số mặt phẳng đối xứng của hình tứ diện đều.
Lời giải: Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện. Vì vậy, hình tứ diện đều sẽ có được 6 mặt phẳng đối xứng.
Bài 4: Cho tứ diện đều ABCD cạnh a. Tính góc giữa AB và CD?
Bài 5: Cho ABCD là tứ diện đều, cạnh a. Kéo dãn BC 1 đoạn CE = a. Kéo dãn BD 1 đoạn DF = a. M là trung điểm của AB.
a. Tìm tiết diện của tứ diện với mp(MEF).
b. Tính diện tích S của tiết diện theo a.
–
Trên đây VnDoc.com đã giới thiệu tới độc giả tài liệu: Thể tích tứ diện đều. Nội dung bài viết giúp tất cả chúng ta nắm được nội dung khái niệm về tứ diện đều là tứ diện có 4 mặt là tam giác đều, nhận mặt được những tính chất của tứ diện đều. Hi vọng qua nội dung bài viết độc giả có thể học tập tốt hơn môn Toán lớp 11 nhé. Để sở hữu kết quả mạnh hơn trong học tập, VnDoc xin giới thiệu tới các bạn học trò tài liệu Trắc nghiệm Toán 11
- Hình lăng trụ là gì? Lăng trụ tam giác đều, tứ giác đều, lục giác
- Khối hệ thống tri thức hình Oxyz
- Bảng công thức lượng giác dùng cho lớp 10 – 11 – 12
- Trọng tâm của tứ diện là gì?
- Bài toán tính tổng của dãy số có quy luật Toán 11
- Công Thức Toán 11 đầy đủ
- Bài tập trắc nghiệm Toán 11: Một số phương trình lượng giác thường gặp


