Đường cao là một đường thẳng có tính chất quan trọng trong tam giác và liên quan rất nhiều tới những bài toán hình học phẳng. Vậy đường cao là gì? Phương pháp tính đường cao trong tam giác? Tính chất đường cao trong tam giác như nào?… Trong nội dung nội dung bài viết sau này, DINHNGHIA.COM.VN sẽ giúp cho bạn tổng hợp tri thức về chủ đề đường cao là gì, cùng tìm hiểu nhé!.

Khái niệm đường cao là gì ?

Trong toán học, đường cao của một tam giác theo khái niệm đây chính là đoạn thẳng kẻ từ một đỉnh và vuông góc với cạnh đối diện. Cạnh đối diện này thường được gọi là đáy tương ứng với đường cao.

Theo lý thuyết, giao điểm của đường cao với đáy thì được gọi là chân của đường cao.

Độ dài của đường cao theo khái niệm đây chính là khoảng tầm cách giữa đỉnh và đáy.

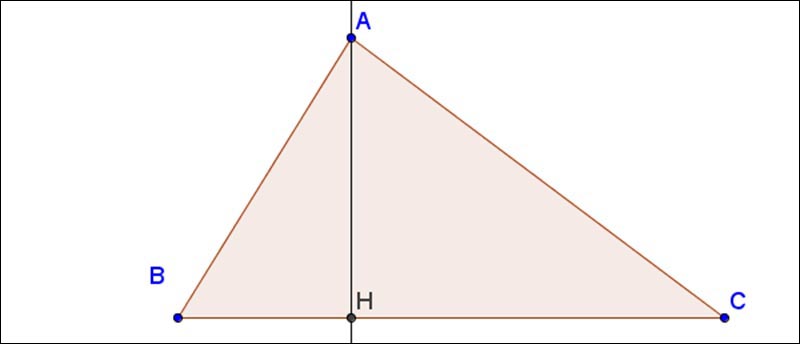
Tìm hiểu tính chất đường cao trong tam giác

Thông thường thì trong tam giác, đường cao sẽ tiến hành sử dụng để tính diện tích S tam giác

Cho tam giác ABC có đường cao AH tương ứng với cạnh đáy BC . Khi đó diện tích S tam giác ABC được tính theo công thức:

SΔABC=1/2*BC*AH

Công thức trên cũng thường được sử dụng để tính độ dài đường cao dựa trên diện tích S tam giác: AH=2*SΔABC/BC

Ví dụ 1:

Cho tam giác ABC đường cao AH . Lấy M là trung điểm AC. . Kẻ MK vuông góc với BC . Biết HBHC=13, tính tỉ số SΔMKCSΔABC

Cách giải:

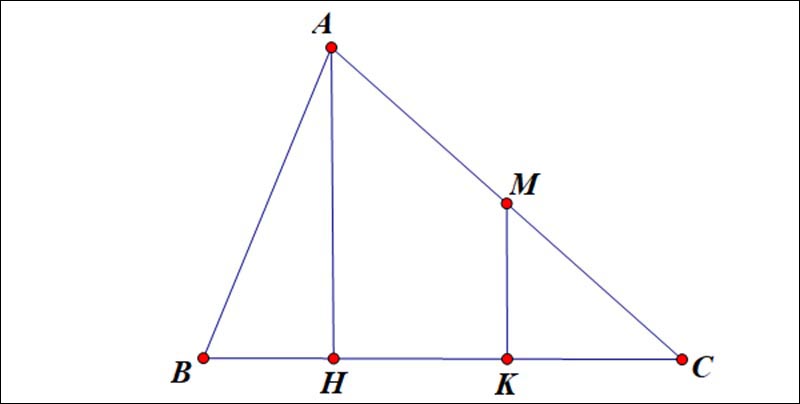
Vì {MK⊥BCAH⊥BC⇒AH||BC)

Mà vì M là trung điểm AC nên ⇒MK là đường trung bình của tam giác AHC

⇒K là trung điểm của HC

⇒KCHC=12

Vì HBHC=13⇒HCBC=34

⇒KCBC=38

Do MK là đường trung bình của tam giác AHC nên MKAH=12

Vậy ta có :

SΔMKC/SΔABC=MK*KC/AH*BC=MK/AH*KC/BC=12*38=316

Tính chất đường cao trong tam giác cân

Trong tam giác cân, theo khái niệm, đường cao tương ứng với cạnh đáy đây chính là đường trung tuyến ứng với cạnh đáy đó. Như vậy, đường cao của tam giác cân đi qua trung điểm của cạnh đáy.

Ngoài ra, đường cao của tam giác cân song song cũng là đường phân giác của góc ở đỉnh và đường trung trực của đáy tam giác.

Trái lại nếu như một tam giác các có đường cao song song cũng là đường trung tuyến hoặc phân giác thì tam giác đó đây chính là tam giác cân.

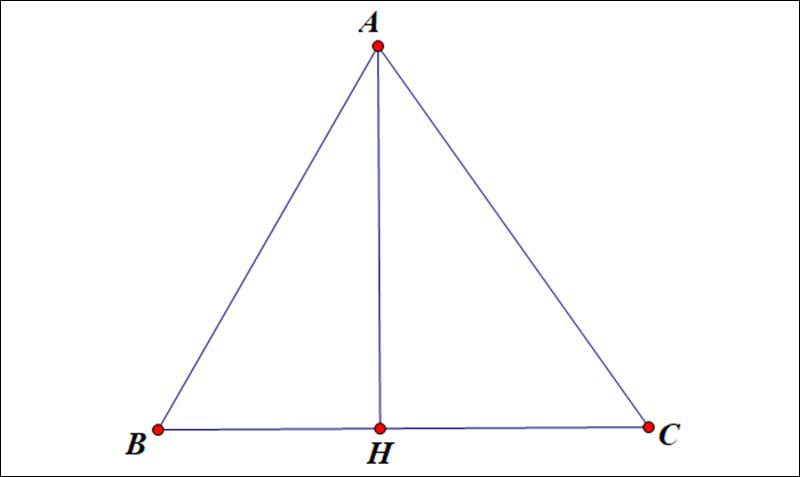
Ví dụ 2:

Cho tam giác ABC đường cao AH và HC=2HB . Trên tuyến đường thẳng đi qua C song song với AH , lấy điểm K sao cho CK=AH và K nằm khác phía với A qua BC . AK∩BC=D. Chứng minh tam giác ABD cân

Cách giải:

Vì

Mà AH=CK⇒AHCK là hình bình hành

⇒D là trung điểm của HC

⇒HDHC=12=HBHC⇒HB=HD

⇒ AH là đường trung tuyến của tam giác ABD

Mà AH cũng là đường cao của tam giác ABD

⇒ tam giác ABD cân tại A

Lưu ý: Tam giác đều là một dạng đặc biệt quan trọng của tam giác cân. Do đó, tính chất đường cao trong tam giác đều cũng tương tự như tính chất đường cao trong tam giác cân.

Tính chất đường cao trong tam giác vuông

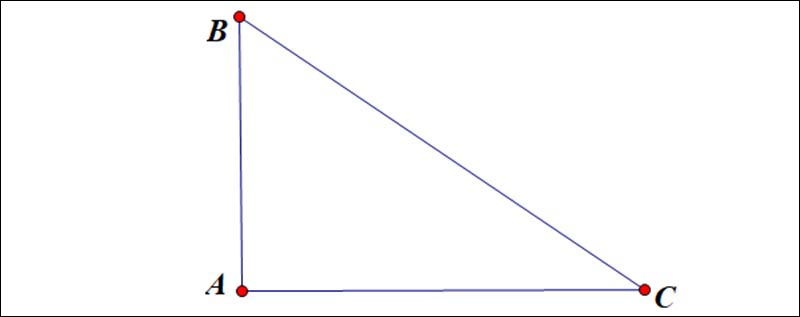
Trong tam giác vuông thì đường cao với đáy là một cạnh góc vuông đây chính là cạnh góc vuông sót lại. Như vậy thì đỉnh góc vuông đây chính là chân đường cao hạ từ hai đỉnh sót lại xuống hai cạnh góc vuông của tam giác.

Tính chất đường cao trong tam giác đều

Tìm hiểu các công thức tính đường cao trong tam giác

Công thức Heron: Đây là công thức tổng quát để tính độ dài đường cao của tam giác bất kỳ

ha=2p(p−a)(p−b)(p−c)√a

Trong số đó:

• a,b,c là độ dài ba cạnh của tam giác
• p là nửa chu vi: p=a+b+c2
• ha là độ dài đường cao tương ứng với cạnh đáy a

Ngoài ra trong một số tam giác đặc biệt quan trọng ta có thể sử dụng các công thức khác để tính đường cao tam giác.

Công thức tính đường cao trong tam giác cân

AH=sqrt(AB^2−(BC^2)/4)

Công thức tính đường cao trong tam giác đều

AH=sqrt(AB^2−(BC^2)/4)=a√3/4

Công thức tính đường cao trong tam giác vuông

Dựa vào hệ thức lượng trong tam giác vuông, ta có thể tính độ dài đường cao bằng những công thức như sau:

AH=AB*AC/BC

AH=sqrt(HB*HC)

1/AH^2=1/AB^2+1/AC^2

Ví dụ 3:

Cho tam giác ABC cân tại A có đường cao AH và BK. Chứng minh rằng :

1/BK^2=1/BC^2+1/4AH^2

Cách giải:

Dựng đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D . Khi đó ta có :

{AH⊥BCBD⊥BC⇒AH||BD

Vì tam giác ABC cân tại A nên đường cao AH cũng là trung tuyến của BC

⇒H là trung điểm BC

⇒AH là đường trung bình của tam giác BCD

⇒BD=2AH

Vận dụng hệ thức lượng với tam giác vuông BCD ta có :

1/BK^2=1/BC^2+1/BD^2=1BC2+1/4AH^2

Tìm hiểu về trực tâm tam giác

Khái niệm trực tâm là gì?

Trực tâm của tam giác hiểu đơn giản đây chính là giao của ba đường cao xuất phát từ ba đỉnh của tam giác đó, song song vuông góc với cạnh đối diện. Ba đường cao này sẽ giao nhau tại một điểm, ta gọi đó là trực tâm của tam giác.

• Khi đối chiếu với tam giác nhọn: Trực tâm sẽ nằm ở miền trong tam giác đó.
• Khi đối chiếu với tam giác vuông: Trực tâm sẽ đây chính là đỉnh góc vuông.
• Khi đối chiếu với tam giác tù: Trực tâm sẽ nằm ở miền ngoài tam giác đó.

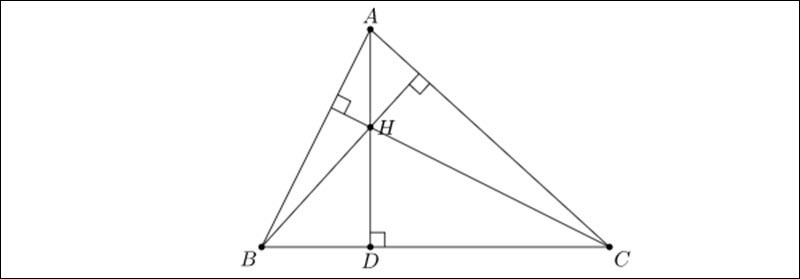
Tính chất trực tâm tam giác

Trực tâm của tam giác có tính chất gì? Đây là vướng mắc mà nhiều học trò quan tâm. Cùng tìm hiểu về tính chất chất trực tâm của tam giác sau này:

Trong tam giác đều thì trực tâm cũng song song đây chính là trọng tâm, và cũng là tâm đường tròn nội tiếp và ngoại tiếp của tam giác đó.

Theo định lý Carnot: Đường cao kẻ từ một đỉnh của tam giác sẽ cắt đường tròn ngoại tiếp của tam giác đó tại điểm thứ hai là đối xứng của trực tâm qua cạnh đáy tương ứng.

Khoảng tầm cách từ một nơi đến trực tâm của tam giác sẽ bằng hai lần khoảng tầm cách từ tâm đường tròn ngoại tam giác đó đến cạnh nối của hai đỉnh sót lại.

Chứng minh tính chất trực tâm tam giác

• Gọi H là trực tâm tam giác ABC . Dựng đường kính BD . Kẻ OI/botBC
• Vì BD là đường kính ⇒BCDˆ=90∘
• ⇒DC⊥BC. Mà AH⊥BC
• ⇒AH||CD
• Tương tự có AD||CH do cùng vuông góc với AB
• Vậy ⇒AHCD là hình bình hành
• ⇒AH=CD(1)

Xét ΔBCD có :

• O là trung điểm BD
• OI||CD do cùng vuông góc với BC
• ⇒OI là đường trung bình của tam giác BCD
• ⇒OI=CD2(2)
• Từ (1)(2)⇒AH=CD=2OI

Ví dụ 4:

Cho tam giác ABC nội tiếp đường tròn(O) . Dựng đường cao AN,CK . Đường tròn ngoại tiếp tam giác BKN cắt (O) tại điểm thứ hai M . Gọi I là trung điểm AC . Chứng minh rằng IM⊥IB

Cách giải:

Lấy J là trung điểm BH

Vì BKHˆ=BNHˆ=90∘⇒ tứ giác BNHK nội tiếp đường tròn đường kính BH

⇒BMHˆ=90∘ hay BM⊥MH(1)

Theo tính chất trực tâm ta có :

OI=BH2=JH

Mặt khác : {OI⊥ACJH⊥BC⇒OI||JH

⇒OIHJ là hình bình hành

⇒HI||OJ(2)

Do J là tâm đường tròn ngoại tiếp tam giác BMH nên ta có :

JM=JB

Mặt khác OM=OB

⇒OJ là đường trung trực của BM

⇒OJ⊥BM(3)

Từ (2)(3)⇒HI⊥BM

Mà từ (1) có MH⊥BM

Từ đó ⇒I,H,M và IM⊥MB

Xem thêm:

• Hình thang cân: Tính chất, Tín hiệu nhận diện và Cách chứng minh
• 5 Công thức tính diện tích S tam giác thường, vuông, cân, vuông cân
• Tính chất tam giác cân: Lý thuyết và Các dạng bài tập

Nội dung bài viết trên đây đã hỗ trợ bạn tổng hợp lý thuyết và các phương pháp giải bài toán liên quan đến đường cao trong tam giác. Hy vọng tri thức trong nội dung bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu về chuyên đề đường cao là gì. Chúc bạn luôn học tốt!.