Đồng quy là gì? Là một trong những lớp học học quan trọng được nhắc tới trong Toán học 7 và tìm hiểu rõ ràng và cụ thể ở Toán học 8,9. Để giải được những bài tập chứng minh đường thẳng đồng quy, thì những bạn học trò cần phải nắm chắc khái niệm, tính chất. Cùng khám phá nội dung thông tin rõ ràng và cụ thể tại chỗ này của ruaxetudong.org!

Đồng quy là gì?

Đồng quy là gặp nhau tại một điểm. Ba đường cao trong một tam giác sẽ đồng quy tại 1 điểm. Điểm này được gọi là trực tâm tam giác. Tính chất của đồng quy 3 đường chéo trong tam giác: “nếu hai tuyến đường cao trong tam giác cắt nhau tại một điểm thì đường cao thứ 3 sẽ đi qua giao điểm đó. Đó là khái niệm khi nhắc tới khái niệm đồng quy trong môn toán hình học.

Trong môn toán đại số, đồng quy là cách chứng minh ba đường thẳng bất kỳ đông quy tại một điểm. Đâu tiên, cần phải tìm giao điểm của hai trong số 3 đường thẳng, sau đó chứng minh đường thẳng còn sót lại cũng đi qua giao điểm đó.

Hai tam giác đồng dạng là gì? Chứng minh hai tam giác đồng dạng

Tính chất của 3 đường thẳng đồng quy là gì toán 7

• Nếu 2 đường cao trong tam giác cắt nhau tại một điểm thì đường cao thứ 3 cũng sẽ đi qua giao điểm đó.
• Ba đường trung tuyến trong tam giác đồng quy tại một điểm, điểm này được gọi là trực tâm của tam giác.
• Ba đường cao của một tam giác đồng quy tại 1 điểm cũng được gọi là trực tâm của tam giác.
• Nếu như 2 đường trung tuyến trong tam giác cắt nhau tại một điểm thì đường trung tuyến thứ 3 cũng sẽ đi qua giao điểm đó. Trọng tâm chia đoạn thẳng trung tuyến đó thành 3 phần từ trong tâm đến đỉnh chiến 2/3 độ dài trung tuyến đó.
• Ba đường phân giác của một tam giác đồng quy tại một điểm được gọi là tâm đường tròn nội tiếp tam giác.
• Nếu như 2 đường phân giác trong tam giác cắt nhau tại một điểm thì đường phân giác thứ 3 cũng sẽ đi qua giao điểm đó. Giao điểm 3 đường phân giác sẽ cách đều 3 cạnh của tam giác.
• Ba đường trung trực trong một tam giác đồng quy tại 1 điểm, điểm này được gọi là đường tròn ngoại tiếp tam giác.
• Nếu như hai tuyến đường trung trực trong tam giác cắt nhau tại một điểm thì đường trung trực thứ 3 sẽ đi qua giao điểm đó, giao điểm 3 đường trung trực cách đều 3 đỉnh tam giác.

Trực tâm là gì? Tính chất, cách xác định trực tâm trong tam giác

Tham dự để 3 đường thẳng đồng quy

Định lý trong tâm: Ba đường trung tuyến của tam giác sẽ cắt nhau tại 1 điểm, khoảng chừng cách từ điểm này tới đỉnh sẽ gấp đôi khoảng chừng cách từ điểm này đến trung điểm của cạnh đối diện. Giao điểm được nhắc tới được gọi là trọng tâm của hình tam giác.

Định lý tâm ngoại tiếp: Các đường trung trực của 3 cạnh tam giác cắt nhau tại một điểm được gọi là tâm ngoại tiếp tam giác.

Định lý trực tâm: Ba đường cao của tam giác cắt nhau tại một điểm được gọi là trực tâm của tam giác.

Định lý tâm nội tiếp: Ba đường phân giác trong tam giác cắt nhau tại 1 điểm gọi là tâm nội tuyến tam giác.

Định lý tâm bàng tiếp: Tia phân giác của góc trong tam giác và tia phân giác của góc ngoài ở hai đỉnh còn sót lại cắt nhau tại 1 điểm. Điểm này được gọi là tâm bàng tiếp của tam giác. Một tam giác sẽ cso 3 tầm bàng tiếp.

=> Trực tâm, trọng tâm, tâm ngoại tiếp, tâm nội tiếp và tâm bàng tiếp đều là tâm của tam giác, chúng có mối liên hệ chặt chẽ với nhau.

Đường trung tuyến là gì? Khái niệm, công thức tính

Cách chứng minh đường thẳng đồng quy trong toán học

Để chứng minh 3 đường thẳng đồng quy, bạn vận dụng một trong số các phương pháp sau:

• Tìm giao của 2 đường thẳng, sau đó chứng minh đường thẳng thứ 3 đi qua giao điểm đó.
• Sử dụng tính chất đồng quy tam giác:
• 3 đường trung tuyến của tam giác đồng quy tại trọng tâm của tam giác
• 3 đường phân giác đồng quy tại tâm đường tròn ngoại tiếp tam giác
• 3 đường trung trực đồng quy tại tâm đường tròn nội tiếp tam giác
• 3 đường cao đồng quy tại trực tâm tam giác.
• Ba điểm trực tâm, trọng tâm và tâm đường tròn ngoại tiếp thẳng hàng thì đường thẳng đi qua 3 điểm này được gọi là đường thẳng Euler của tam giác.
• Sử dụng định lý Ceva: Cho tam giác ABC và 3 điểm bất kì M, N, P. nằm trên cạnh BC, CA, AB. Khi đó 3 đường thẳng AM, BN, CP sẽ đồng quy khi và chỉ khi:

Hình chóp là gì? Công thức chu vi, diện tích S, thể tích hình chóp

Một số bài tập về đồng quy trong toán học 8,9

Bài tập 1: Cho tam giác ABC cân tại A, lấy điểm D thuộc cạnh AB, kẻ DE song song với BC (E thuộc AC). Gọi M là trung điểm của BC. Hãy chứng minh AM, BE, CD đồng quy

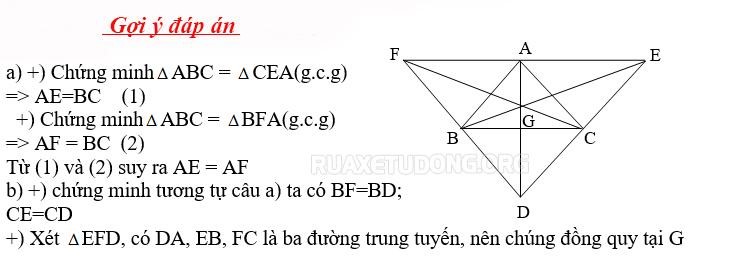
Bài tập 2: Cho tam giác ABC, qua mỗi đỉnh A, B, C kẻ đường cao song song với cạnh đối diện, cắt nhau tạo thành tam giác DEF

a, Chứng minh A là trung điểm của EF

b, Chứng minh AD, BE,CF đồng quy

Bài tập 3: Cho hai tuyến đường tròn (O) và (O’) cắt nhau tại A và B. Các đường thẳng AO, AO’ cắt (O) tại C và D và cắt (O’) tại E và F. Chứng minh AB, CD, EF đồng quy

Hy vọng rằng, các thông tin rõ ràng và cụ thể có trong nội dung bài viết “Đồng quy là gì? Tìm hiểu về đồng quy, đường thẳng đồng quy trong toán học” sẽ giúp ích bạn. Để sở hữu thêm nhiều thông tin hữu ích về Toán học, quý bạn được hãy truy cập website ruaxetudong.org, kiên cố sẽ giúp ích bạn rất nhiều đó!