• BTV
• Nội dung bài viết

Độ lệch chuẩn là gì?

Độ lệch chuẩn hay còn gọi là Standard Deviation. Là đại lượng dùng để làm phản ánh độ phân tán của khá nhiều giá trị trong bộ tài liệu. Thể hiện sự biến thiên của giá trị trong một thời khắc phản ánh xu thế của việc thay đổi.

Khi hai tập tài liệu có cùng giá trị trung bình cộng, tập nào có độ lệch chuẩn to ra thêm là tập có tài liệu biến thiên nhiều hơn. Trong trường hợp hai tập tài liệu có mức giá trị trung bình cộng không bằng nhau, thì việc so sánh độ lệch chuẩn của chúng không có ý nghĩa.

Thông qua độ lệch chuẩn các nhà tài chính, nhà quản lý có thể quan sát dự báo các thời kỳ biến động của nền tài chính. Khi đối chiếu với các ngành khác cũng tương tự, độ lệch chuẩn luôn phân tích tính ổn định hoặc sự thay đổi cụ thể nào đó.

Công thức tính độ lệch chuẩn

Công thức tính độ lệch chuẩn được thể hiện dưới dạng công thức:

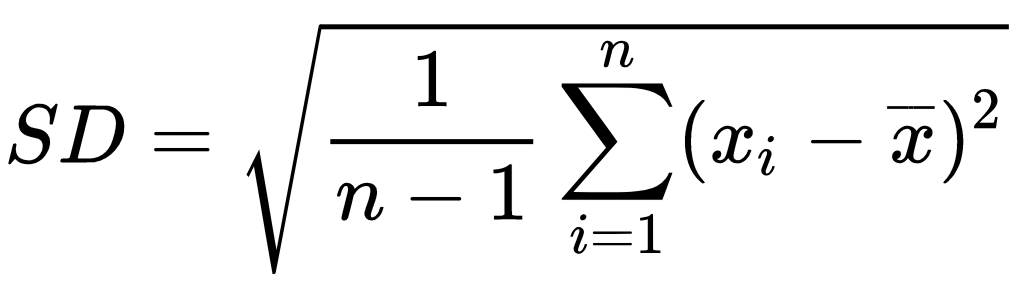
Trong số đó:

• – SD là độ lệch tiêu chuẩn
• – xi là kết quả quan sát thứ i của mẫu
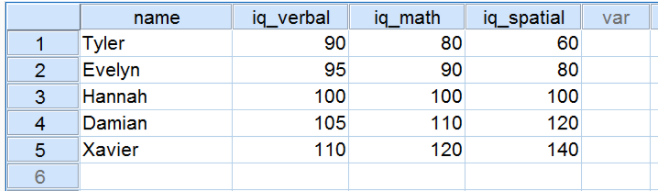• – là giá trị trung bình của khá nhiều quan sát này
• – n là số lượng quan sát trong mẫu.

Các bước tính độ lệch chuẩn

Tính trung bình

Để tính giá trị trung bình tất cả chúng ta sẽ lấy tổng các giá trị trong một bộ tài liệu xác định chia cho tổng số những giá trị mà tất cả chúng ta có trong bộ tài liệu đó.

Ví dụ: Tập hợp những điểm cho một bài kiểm tra là: 10, 8, 10, 8, 8, và 4.

=> Tính giá trị trung bình: Lấy trung bình cộng của 10, 8, 10, 8, 8, và 4. Bạn thấy có 6 số liệu trong tập hợp điểm kiểm tra này và tổng của khá nhiều số đó là 48. Như vậy kết quả trung bình cộng thu được là 48 / 6 = 8.

Tính phương sai

Tất cả chúng ta sẽ tiến hành chia ra nhiều bước vì tính phương sai khá phức tạp và cần cẩn thận.

Bước 1: Trước nhất, lấy giá trị trung bình đã được được tính ở trên trừ đi từng giá trị cụ thể trong bộ tài liệu. Như vậy tất cả chúng ta sẽ có được kết quả là khoảng chừng cách của từng giá trị so với giá trị trung bình đã tìm được.

Bước 2: Bình phương những giá trị vừa mới được tính khi thực hiện phép trừ ở phía trên.

Ví dụ với tập hợp những điểm 10, 8, 10, 8, 8, và 4 và giá trị trung bình là 8. Khi bình phương các phép trừ sẽ theo trật tự là 4, 0, 4, 0, 0, và 16.

Bước 3: Tìm tổng bình phương bằng phương pháp cộng tất cả những giá trị sau khoản thời gian bình phương ở trên.

Tập hợp các số liệu lúc đầu tất cả chúng ta đã sở hữu được tổng bình phương là: 4 + 0 + 4 + 0 + 0 + 16 = 24.

Bước 4: Tìm được phương sai bằng phương pháp đem tổng bình phương chia cho một số cụ thể. Số này được tính bằng phương pháp lấy tổng số các giá trị trừ đi 1.

Với tập hợp điểm kiểm tra lúc đầu tất cả chúng ta có tổng số các giá trị là 6, tổng bình phương là 24. Vậy phương sai của cục số liệu này là kết quả của phép tính 24/ (6-1) = 4,8.

Tính độ lệch chuẩn

Độ lệch chuẩn sẽ tiến hành tính bằng căn bậc 2 của phương sai. Sau khoản thời gian đã tính được phương sai thì tất cả chúng ta sẽ dễ dàng tính được độ lệch chuẩn.

Trong bộ tài liệu tất cả chúng ta đã chọn lúc đầu. Với giá trị phương sai là 4, 8.

=> Giá trị của độ lệch chuẩn sẽ là: √4,8 = 2,19.

Ý nghĩa của độ lệch chuẩn

Độ lệch chuẩn là một phương tiện đặc biệt quan trọng hữu ích trong chiến lược góp vốn đầu tư và thanh toán giao dịch vì nó giúp giám sát sự biến động của thị trường và dự đoán xu hướng.

Độ lệch chuẩn đo tính biến động của giá trị mang tính thống kê. Nó cho thấy sự chênh lệch về giá trị của từng thời khắc nhìn nhận và đánh giá so với giá trị trung bình. Tính biến động cũng như độ lệch chuẩn sẽ lơn hơn nếu giá đóng cửa và giá đóng cửa trên trung bình khác nhau đáng kể.

Nếu sự chênh lệch không đáng kể thì độ lệch chuẩn và tính biến động tại mức thấp. Sự đảo chiều xu thế tạo các vùng đáy hoặc đỉnh của thị trường được xác định thời cơ bằng các mức độ biến động cao.

Những xu thế mới của giá sau thời kỳ thoái trào của thị trường (tức là thời đoạn kiểm soát và điều chỉnh) thường được xác định thời cơ bằng những mức độ biến động thấp. Sự thay đổi đáng kể về tài liệu giá đem lại giá trị độ lệch chuẩn cao và tài liệu giá ổn định hình thành độ lệch chuẩn tại mức thấp.

Ví dụ về Độ lệch chuẩn – Ví dụ 1

Giả sử tất cả chúng ta có những số: 5, 7, 3 và 7, tổng của chúng = 22.

• Lấy 22 chia cho số lượng các số, trong trường hợp này là 4 được 5,5.
• Tất cả chúng ta có trung bình là: x̄ = 5,5 và N = 4.

Phương sai sẽ tiến hành xác định bằng phương pháp trừ mỗi số cho giá trị trung bình. Từ đó, tuần tự các kết quả là: -0,5, 1,5, -2,5 và 1,5.

Lấy các giá trị đó bình phương lên, kết quả: 0,25, 2,25, 6,25 và 2,25.

Tiếp đến, cộng các giá trị bình phương sau đó chia cho giá trị N trừ 1, bằng 3. => Cho kêt quả phương sai xấp xỉ = 3,67. Căn bậc hai của phương sai có độ lệch chuẩn là khoảng chừng 1.915.

Ví dụ về Độ lệch chuẩn – Ví dụ 2

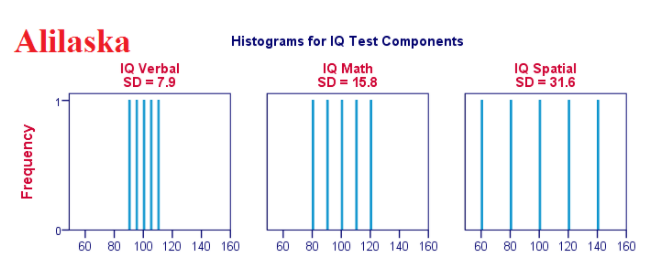
Năm ứng viên đã làm bài kiểm tra IQ như một phần của đơn xin việc. Điểm số của họ trên ba thành phần IQ được hiển thị sau này.

Hiện tại hãy xem xét kỹ điểm số của 3 thành phần Q.. Lưu ý rằng cả ba đều phải sở hữu trung bình 100. Tuy nhiên, điểm số trên iq verbal năm gần nhau hơn so với điểm số trên ig_math. Hơn nữa, điểm số trên iq_spatial nằm cách xa nhau hơn so với điểm số của hai thành phần trước hết. Mức độ xác thực mà một số điểm nằm ngoài có thể được biểu thị bằng một số lượng Số lượng này được gọi là độ lệch chuẩn

Trong cuộc sống thực, rõ ràng tất cả chúng ta không kiểm tra trực ý kiến số thô để xem chúng cách nhau bao xa. Thay vào đó, tất cả chúng ta chỉ đơn giản dùng một số phần mềm tính toán. Bảng sau này cho thấy độ lệch chuẩn và một số thống kê khác cho tài liệu IQ trên. Lưu ý rằng độ lệch chuẩn xác nhận mẫu tất cả chúng ta đã thấy trong tài liệu thô.

Ví dụ về Độ lệch chuẩn – Biểu đồ trực quan

Hình sau này cho thấy độ lệch chuẩn và biểu đồ cho điểm IQ. Lưu ý rằng mỗi thanh đại diện thay mặt cho điểm của một ứng viên trên 1 thành phần IQ. Một lần nữa, tất cả chúng ta thấy rằng độ lệch hợp lý cho thấy mức độ của những điểm nằm cách nhau.

Khi tất cả chúng ta hình dung tài liệu trên một số ít các quan sát như trong hình trước, tất cả chúng ta dễ dàng nhìn thấy một hình ảnh rõ ràng. Để sở hữu một ví dụ thực tế hơn, hãy quan sát biểu đồ cho một.000 quan sát phía bên dưới. Nhấn mạnh vấn đề, các biểu đồ này còn có quy mô y sì nhau; so với mỗi biểu đồ, một centimet trên trục X tương ứng với khoảng chừng 40 điểm thành phần IQ.

UniTrain tổng hợp

Xem thêm

Combo 3 khóa học Data Analytics for Professionals