Trong quy trình phân tích, khi những thước đo trình diễn vị trí/xu thế “trung tâm” (mean, median, mode) của 2 tập tài liệu có mức giá trị xấp xỉ đều bằng nhau, ta sẽ gặp khó khăn khi cần tìm thấy nhận xét, review sự khác lạ của 2 tập tài liệu. Lúc này, những đại lượng đo mức độ phân tán của tài liệu sẽ có được ích hơn trong việc review.
Trong nội dung bài viết này, 6 đại lượng đo mức độ phân tán của tập tài liệu sẽ tiến hành reviews:
- Bách phân vị (Percentile)
- Tứ phân vị (Quartile)
- Khoảng chừng biến thiên (Range)
- Khoảng chừng trải giữa (InterQuartile Range)
- Phương sai (Variance)
- Độ lệch chuẩn chỉnh (Standard deviation)
Những đại lượng này sẽ hỗ trợ ích trong việc đo lường và thống kê mức độ biến thiên, mức độ phân tán và trang trải của tài liệu. Thông qua đó, hoàn toàn có thể rút ra những nhận xét, mô tả bộ tài liệu nghiên cứu và phân tích tương đối đầy đủ và đúng đắn hơn.
1. Khoảng chừng biến thiên (Range)
Khoảng chừng biến thiên (Range) trong thống kê là đại lượng đo mức độ trải dài của một tập tài liệu nhất định từ nhỏ nhất đến lớn số 1. Dễ hiểu hơn, trong một tập tài liệu, khoảng tầm biến thiên là hiệu số giữa giá trị lớn số 1 và giá trị nhỏ nhất.
Công thức tính khoảng tầm biến thiên:
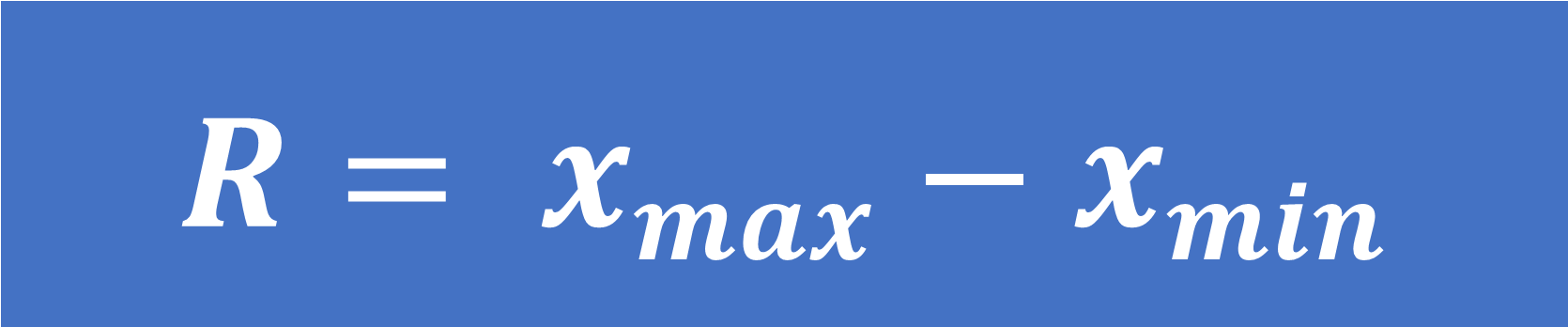
Trong số đó: R là khoảng tầm biến thiên, xmax là giá trị lớn số 1, xmin là giá trị nhỏ nhất
Ví dụ: Cho tập tài liệu X={2,4,5,6,7,8,9,12,15}.
Ta thấy giá trị lớn số 1 của tập X là xmax=15 và giá trị nhỏ nhất là xmin=2 =>Khoảng chừng biến thiên R là:

Trong thực tiễn, ta hoàn toàn có thể thấy khoảng tầm biến thiên được tận dụng trong rất nhiều trường hợp, ví như tìm ra sự phân tán điểm kiểm tra trong một lớp học hay để xác định phạm vi giá cả của một dịch vụ, …
Trong những đại lượng đo mức độ phân tán của tài liệu, khoảng tầm biến thiên là một đại lượng rất dễ hiểu và dễ tính toán. Tuy nhiên, khoảng tầm biến thiên chỉ tận dụng giá trị MAX và MIN của tập tài liệu để tính toán mà không diễn giải được sự phân tán giữa 2 giá trị này. Do đó, nó không phải là một đại lượng hữu ích để review sự phân tán của tập tài liệu vì ta cần xem xét trên toàn bộ tài liệu.
Khoảng chừng biến thiên là thang đo tương đối tốt so với những bộ tài liệu nhỏ như ví dụ trên, nhưng độ tin cậy sẽ ít đi khi ứng dụng với những bộ tài liệu lớn do độ trang trải của tài liệu cũng sẽ to hơn. Một vấn đề cần lưu ý khác là giá trị của khoảng tầm biến thiên sẽ bị tác động bởi những giá trị ngoại lệ (Outliers)[1]. Do đó, không nên tận dụng đại lượng khoảng tầm biến thiên so với những bộ tài liệu có mức giá trị ngoại lệ.
2. Bách phân vị (Percentile) và Tứ phân vị (Quartile)
Bách phân vị (Percentile) Tứ phân vị (Quartile)
ĐỊNH NGHĨA
Bách phân vị (Percentile) là đại lượng dùng làm ước tính tỷ trọng tài liệu trong một tập số liệu rơi vào vùng mạnh hơn hoặc thấp hơn so với một giá trị cho trước. Bách phân vị chia tài liệu có trật tự theo hàng trăm.
Hoàn toàn có thể diễn giải qua ví dụ sau:
Ta có phân vị thứ p∈[0;100] và giá trị vp tại vị trí p thì:
- có ít nhất p% những quan sát có mức giá trị ≤vp
- có ít nhất (100-p)% những quan sát có mức giá trị ≥vp
Ví dụ qua số liệu:
Chẳng hạn tại phân vị thứ 85 của tập tài liệu X có mức giá trị là 20 thì sẽ có được nhiều nhất 85% số quan sát có mức giá trị thấp hơn 20 và có nhiều nhất (100-85)=15% số quan sát có mức giá trị to hơn 20.
Tứ phân vị (Quartile) là một trường hợp quan trọng của bách phân vị. Tứ phân vị có 3 giá trị, đó là tứ phân vị thứ nhất, thứ nhì, và thứ ba. Ba giá trị này chia một tập hợp tài liệu đã sắp xếp theo trật tự thành 4 phần có số lượng quan sát đều nhau.
CÁCH XÁC ĐỊNH
Để xác định giá trị (vp) của phân vị thứ p trong một tập tài liệu, ta tiến hành theo công việc sau:
1. Sắp xếp tài liệu theo trật tự từ nhỏ nhất đến lớn số 1.
2. Tính chỉ số i:
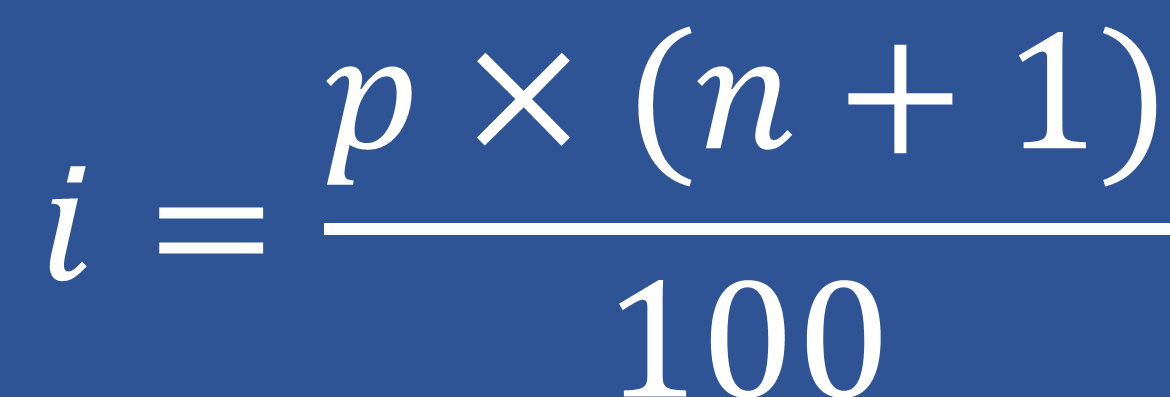
Trong số đó:i là vị trí của giá trị tài liệu tại phân vị thứ pp là phân vị thứ pn là tổng số quan sát
3. Xác định giá trị vp
– Nếu i LÀ số nguyên thì phân vị thứ p là giá trị tài liệu ở vị trí thứ i trong tập tài liệu.
– Nếu i KHÔNG phải là số nguyên thì làm tròn i lên và làm tròn i xuống số nguyên sớm nhất có thể, tiếp sau đó tính trung bình hai giá trị tài liệu ở hai vị trí này trong tập tài liệu.
– Giá trị tứ phân vị thứ nhất Q1 bằng trung vị phần dưới, tương đương với bách phân vị thứ 25.
– Giá trị tứ phân vị thứ hai Q2 chính bằng giá trị trung vị, tương đương với bách phân vị thứ 50.
– Giá trị tứ phân vị thứ ba Q3 bằng trung vị phần trên, tương đương với bách phân vị thứ 75.
VÍ DỤ
Một tập tài liệu bao gồm tất cả 29 trong tuổi dành riêng cho nam diễn viên xuất sắc nhất đoạt Giải Oscar theo trật tự từ nhỏ nhất đến lớn số 1 được cho như sau: X={18; 21; 22; 25; 26; 27; 29; 30; 31; 33; 36; 37; 41; 42; 47; 52; 55; 57; 58; 62; 64; 67; 69; 71; 72; 73; 74; 76; 77}Tìm phân vị thứ 70 và 83?
– Ta có: n = 29, p1=70, p2=83
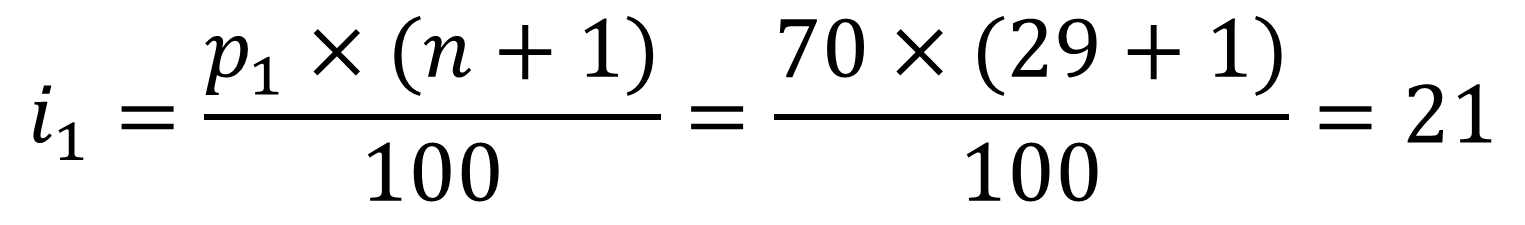
– Vì i1=21 là số nguyên nên ta sẽ tận dụng giá trị tài liệu ở vị trí thứ 21 trong tập tài liệu là 64.
=> Phân vị thứ 70 là 64. Hoàn toàn có thể Kết luận 70% nam diễn viên xuất sắc nhất giành giải Oscar có trong tuổi thấp hơn 64 và 30% nam diễn viên xuất sắc nhất giành giải Oscar trên 64 tuổi.
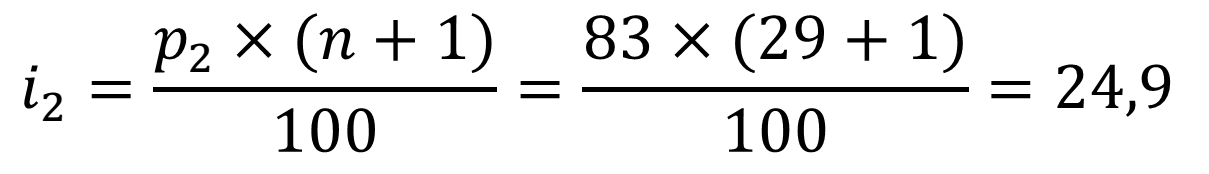
– Vì i2=24,9 không phải là số nguyên nên ta sẽ làm tròn xuống 24 và làm tròn lên 25. Tuổi ở vị trí thứ 24 là 71 và tuổi ở vị trí thứ 25 là 72. Trung bình cộng 71 và 72 là 71,5.
=>Phân vị thứ 83 là 71,5 tuổi.
Một tập tài liệu được cho như sau:X={1; 11,5; 6; 7,2; 4; 8; 9; 10; 6,8; 8,3; 2; 2; 10; 1}Xác định giá trị Q1, Q2 và Q3?.
– Thứ nhất, sắp xếp lại tập X theo trật tự tăng dần: X={1; 1; 2; 2; 4; 6; 6,8; 7,2; 8; 8,3; 9; 10; 10; 11,5}
– Tập tài liệu có 14 quan sát, giá trị trung vị nằm trong lòng giá trị thứ 7 (6,8) và giá trị thứ 8 (7,2). Giá trị trung vị là trung bình cộng của 2 giá trị này:
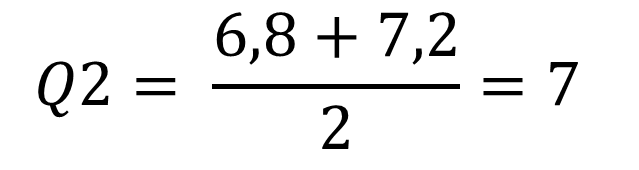
Q1, là giá trị giữa của nửa dưới tài liệu tương ứng với tập tài liệu X1={1; 1; 2; 2; 4; 6; 6,8}. Tập X1 có 7 giá trị, do đó giá trị trung vị của tập tài liệu X1 là 2. => Q1 = 2
Q3, là giá trị nửa trên của tài liệu tương ứng với tập tài liệu X2={7,2; 8; 8,3; 9; 10; 10; 11,5}. Tập X2 có 7 giá trị, do đó giá trị trung vị của tập tài liệu X2 là 9. => Q3 = 9
Kết luận: ¼ tập tài liệu có mức giá trị ≤2, ¾ tập tài liệu có mức giá trị ≥2. Tương tự Kết luận với Q2 và Q3.
ỨNG DỤNG
Bách phân vị được tận dụng trong nhiều nghành nghề như: đo lường và thống kê băng thông internet, thước đo sự phát triển của trẻ em trong y khoa, đo lường và thống kê mốc giới hạn vận tốc, report điểm số tổng quan trong những bài kiểm tra hay trong những nghành nghề tài chính, v.v…
Ví dụ trong y khoa: Một trẻ nam 2 tuổi có độ cao 110cm và khối lượng 13,3kg; khi so sánh với biểu đồ bách phân vị khối lượng và độ cao theo trong tuổi của WHO thì độ cao ở tầm mức bách phân vị 50 và khối lượng ở tầm mức bách phân vị 85.=> Kết luận: Đứa trẻ này mạnh hơn so với 50 trẻ và nặng hơn so với 85 trẻ khác trong 100 trẻ cùng lứa tuổi và nam nữ.
Ngoài những ứng dụng tương tự như bách phân vị, tứ phân vị còn tồn tại hiệu quả kiểm soát tác động của những giá trị ngoại lệ (Outliers) ở cả 2 đầu mút. Để nắm rõ hơn, ta sẽ tiếp tục tìm hiểu trong đại lượng tiếp theo: Khoảng chừng trải giữa (InterQuartile Range)
3. Khoảng chừng trải giữa (InterQuartile Range)
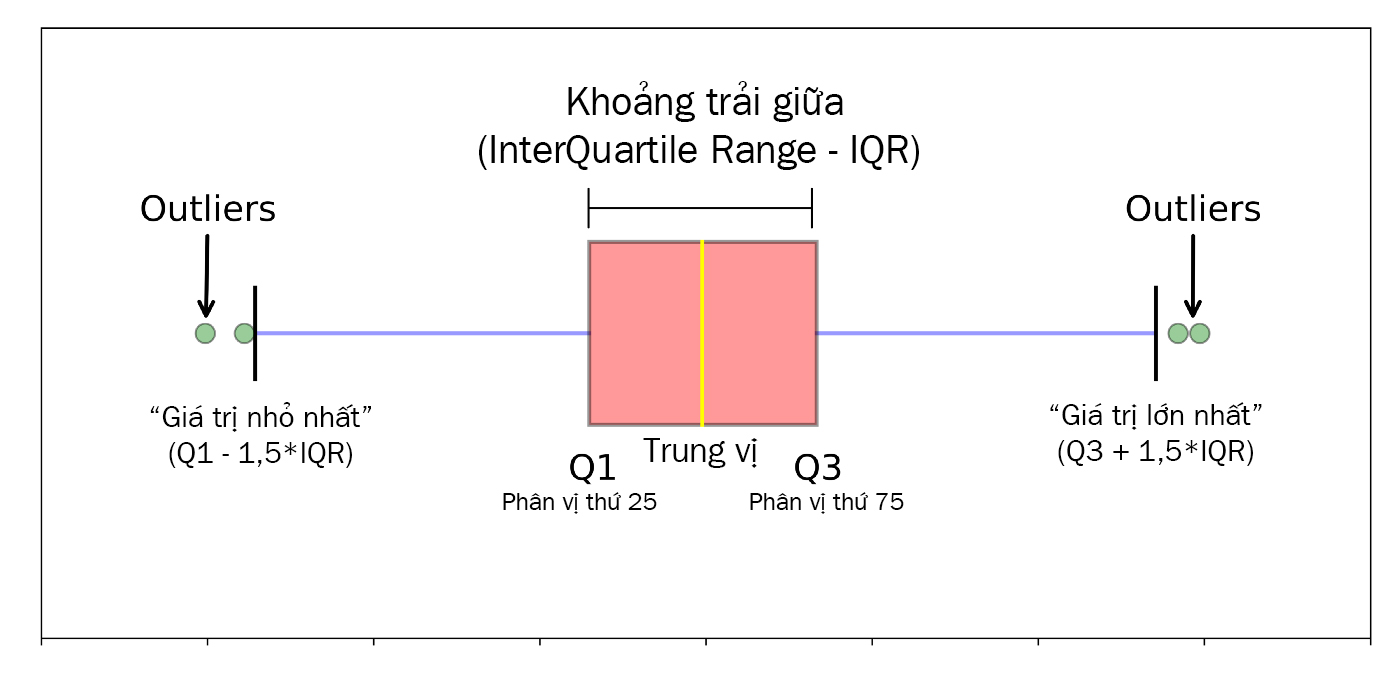
Khoảng chừng trải giữa (InterQuartile Range – IQR) hay còn gọi là khoảng tầm tứ phân vị của tập tài liệu. Khoảng chừng trải giữa là một số lượng cho thấy thêm mức độ Viral của nửa giữa hoặc 50% phần giữa của tập tài liệu. IQR thường được tận dụng thay cho khoảng tầm biến thiên (Range) vì nó loại trừ hồ hết giá trị thất thường hay giá trị ngoại lệ (Outliers) của tài liệu.
Công thức tính IQR có dạng:

IQR hoàn toàn có thể giúp xác định những giá trị ngoại lệ. Một giá trị bị nghi ngờ là một giá trị ngoại lệ nếu nó nhỏ hơn 1,5*IQR dưới phần tư trước tiên (Q1 – 1,5*IQR) hoặc to hơn (1,5*IQR) trên phần tư thứ ba (Q3 + 1,5*IQR) (Xem hình dưới). Những giá trị ngoại lệ luôn luôn yêu cầu việc thanh tra rà soát, kiểm tra lại tài liệu. Những điểm tài liệu quan trọng này hoàn toàn có thể do lỗi hoặc do sự thất thường trong tài liệu nhưng cũng hoàn toàn có thể là vấn đề mẫu chốt để hiểu tài liệu.
4. Phương sai (Variance) và Độ lệch chuẩn chỉnh (Standard deviation)
Trong một trong những tập tài liệu, những giá trị tài liệu được triệu tập gần giá trị trung bình; nhưng trong những tập tài liệu khác, những giá trị tài liệu hoàn toàn có thể được trải rộng hơn so với giá trị trung bình. Phương sai và độ lệch chuẩn chỉnh là 2 thuật ngữ được tận dụng thịnh hành để mô tả sự phân tán này và cả hai đều tìm thấy những giá trị đo lường và thống kê mức độ phân tán của tài liệu xung quanh giá trị trung bình.
Phương sai (Variance) Độ lệch chuẩn chỉnh (Standard deviation)
ĐỊNH NGHĨA
Phương sai (Variance) là thước đo độ biến thiên của những giá trị xung quanh giá trị trung bình số học của chúng, nó cho thấy thêm những giá trị đó ở cách giá trị kỳ vọng bao xa. Một kiểu dễ hiểu hơn, phương sai sẽ cho thấy thêm mức độ chênh lệch trong tập tài liệu.
Phương sai thường được ký hiệu theo tính chất của tập tài liệu:
– So với tài liệu là một tổng thể: phương sai ký hiệu là σ2
– So với tài liệu là mẫu từ tổng thể: phương sai ký hiệu là s2
Độ lệch chuẩn chỉnh (Standard deviation) là thước đo độ phân tán của những giá trị trong một tập tài liệu đã cho từ giá trị trung bình của chúng. Nó cho thấy thêm trung bình mỗi giá trị nằm bao xa so với giá trị trung bình.
Tương tự, độ lệch chuẩn chỉnh cũng rất được ký hiệu:
– So với tài liệu là một tổng thể: phương sai ký hiệu là σ
– So với tài liệu là mẫu từ tổng thể: phương sai ký hiệu là s
CÔNG THỨC TÍNH
Phương sai là giá trị trung bình của bình phương {khoảng cách} của mỗi điểm tài liệu tới điểm trung bình.
– So với tài liệu là một tổng thể:
Công thức tính:
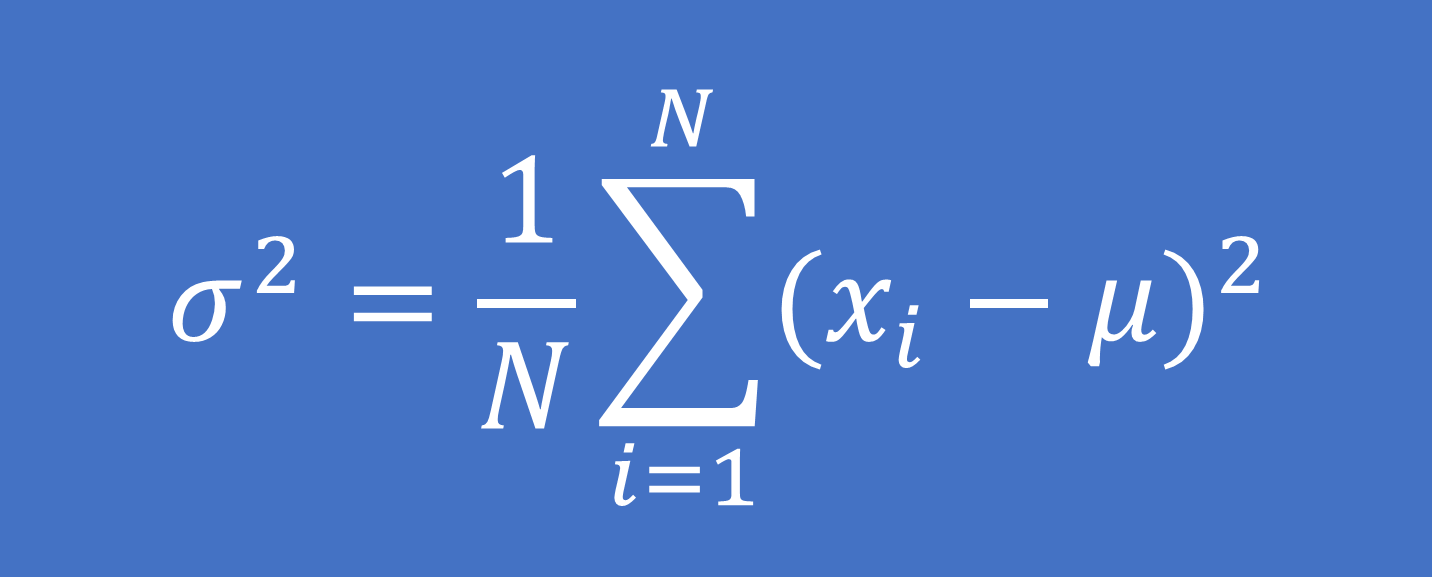
Trong số đó: xi là giá trị của quan sát thứ i
μ là giá trị trung bình tổng thể
N là tổng số quan sát của tổng thể
– So với tài liệu là một mẫu từ tổng thể:
Công thức tính:
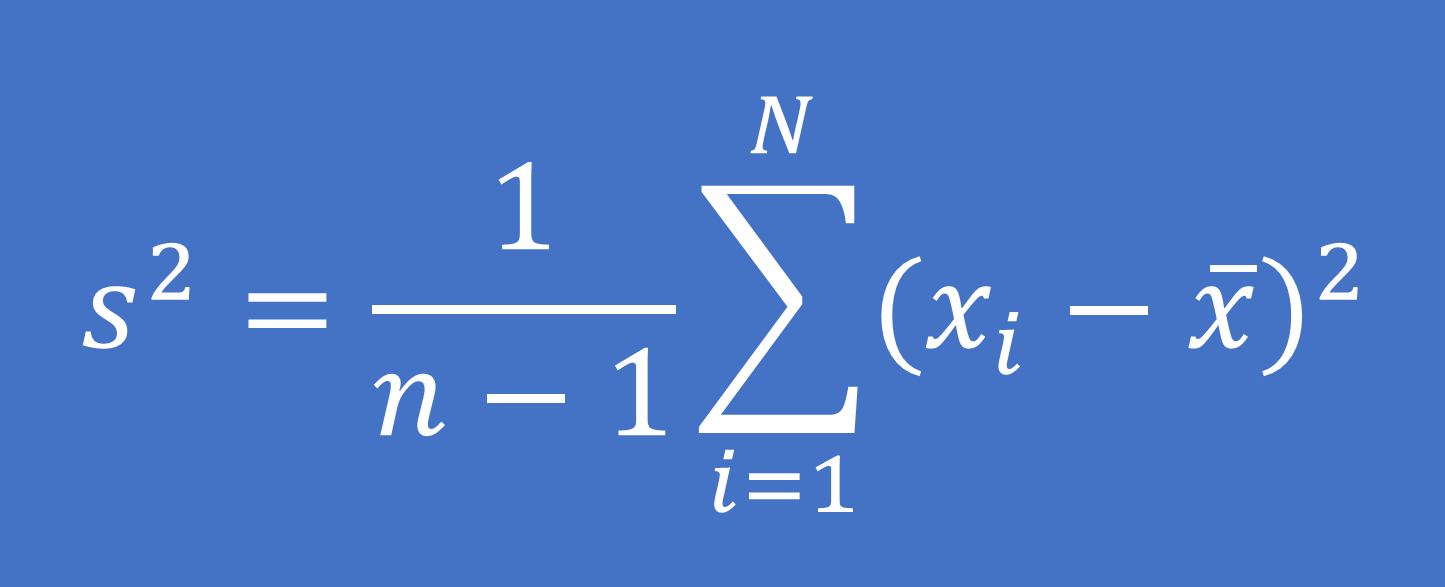
Trong số đó: xi là giá trị của quan sát thứ i
x ̅ là giá trị trung bình của mẫu tài liệu
n là số quan sát trong mẫu tài liệu
Độ lệch chuẩn chỉnh là căn bậc hai của phương sai.
– So với tài liệu là một tổng thể:
Công thức tính:
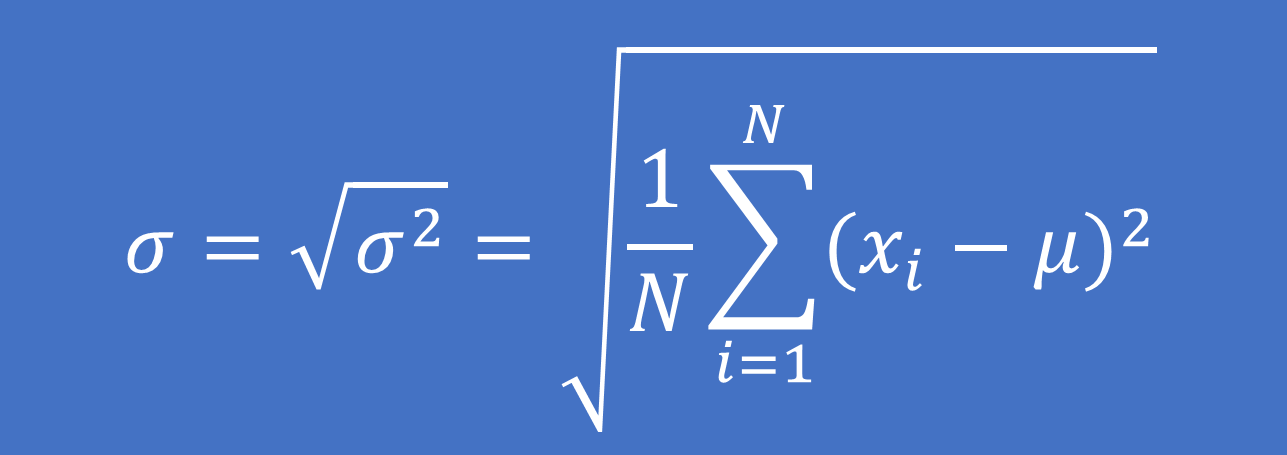
Trong số đó: xi là giá trị của quan sát thứ i
μ là giá trị trung bình tổng thể
N là tổng số quan sát của tổng thể
– So với tài liệu là một mẫu từ tổng thể:
Công thức tính:
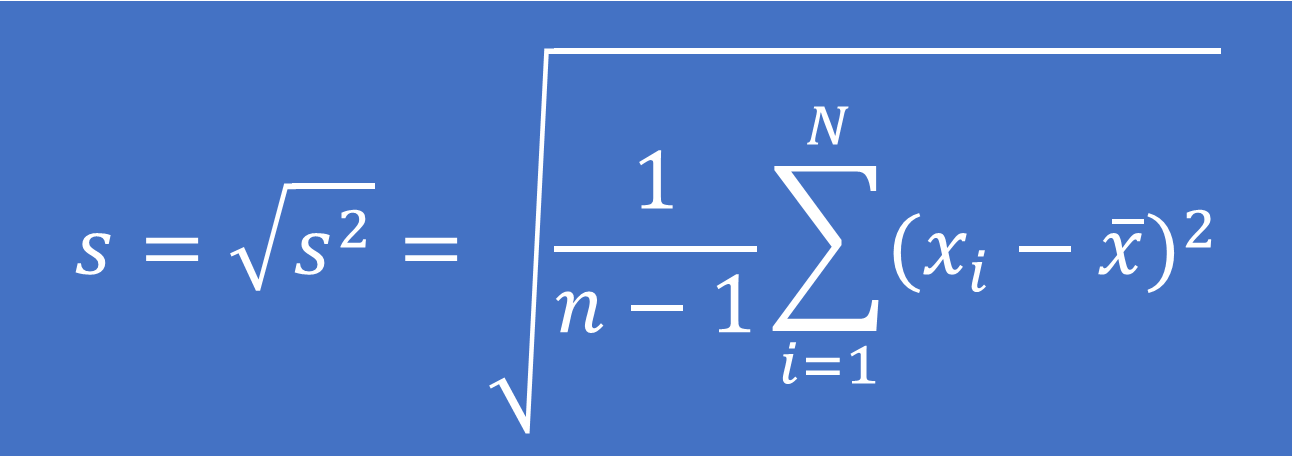
Trong số đó: xi là giá trị của quan sát thứ i
x ̅ là giá trị trung bình của mẫu tài liệu
n là số quan sát trong mẫu tài liệu
VÍ DỤ
Mẫu tài liệu về thời hạn (giây) chạy cự ly 500m và 1500m của một nhóm gồm 5 người:T500 = {55.2, 58.8, 62.4, 54, 59.4}T1500 = {271.2, 261, 276, 282, 270}Tính phương sai chạy 2 cự ly 500m và 1500m.
– Tính giá trị trung bình của 2 mẫu tài liệu:
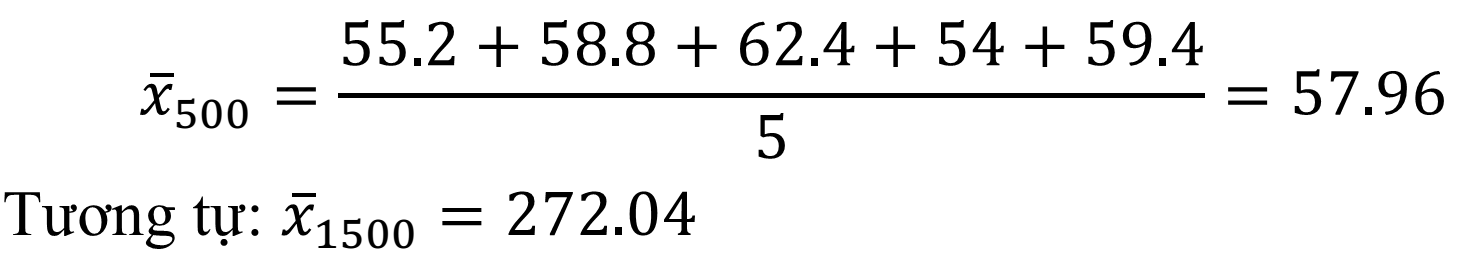
– Phương sai:

=> Kết luận: Phương sai của cự ly 1500m có mức giá trị mạnh hơn cự ly 500m, cho thấy có sự biến động mạnh hơn, tức tài liệu có sự trang trải rộng hơn giữa thời hạn chạy của 5 người này..
Mẫu tài liệu về thời hạn (giây) chạy cự ly 500m và 1500m của một nhóm gồm 5 người:T500 = {55.2, 58.8, 62.4, 54, 59.4}T1500 = {271.2, 261, 276, 282, 270}Tính phương sai chạy 2 cự ly 500m và 1500m.
– Tính giá trị trung bình của 2 mẫu tài liệu:
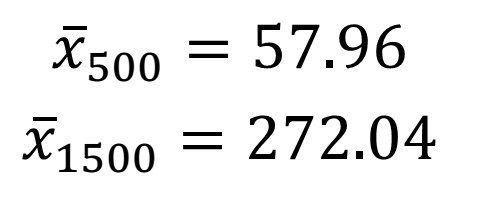
– Độ lệch chuẩn chỉnh:
s500=3.38
s1500=7.77
=> Kết luận: Độ lệch chuẩn chỉnh của cự ly 500m cho thấy thêm thời hạn chạy 500m của 5 người này chỉ lệch trung bình 3.38s so với thời hạn chạy trung bình 500m là 57.96s. Nhưng độ lệch chuẩn chỉnh của cự ly 1500m đến 7.77s cho thấy với cự ly dài ra hơn nữa thì thành tích trung bình của 5 vận động viên sẽ có được sự khác lạ đáng kể hơn so với cự ly 500m.
ỨNG DỤNG
Phương sai được tận dụng trong những nghành nghề như: trong công nghiệp, phương sai biểu thị độ đúng đắn của sinh sản; trong chăn nuôi, nó biểu thị độ đồng đều của những con gia súc; trong trồng trọt, nó biểu thị mức độ ổn định của năng suất; trong tài chính, nó là một thông số quan trọng trong phân chia tài sản đầu tư, giúp những nhà góp vốn đầu tư phát triển danh mục góp vốn đầu tư tốt hơn bằng phương pháp tối ưu hóa sự đánh đổi giữa rủi ro và lợi nhuận với mỗi khoản góp vốn đầu tư, …
Chính vì dễ tưởng tượng và dễ ứng dụng hơn nên độ lệch chuẩn chỉnh thường được tận dụng như một thước đo chính của sự việc thay đổi của những tài liệu trong tập tài liệu.
Độ lệch chuẩn chỉnh được tận dụng cho một trong những nghành nghề như kiểm soát unique thành phầm, dự báo thời tiết, đo lường và thống kê rủi ro biến động trên thị trường tài chính.
Ngoài ra, độ lệch chuẩn chỉnh cũng có thể có hiệu quả giúp chuẩn chỉnh hóa giá trị của những dãy số không giống nhau về cùng 1 miền tài liệu.
LƯU Ý
Phương sai lớn cho thấy có nhiều sự biến động trong những giá trị của tập tài liệu và hoàn toàn có thể có {khoảng cách} to hơn giữa giá trị các quan sát với nhau. Nếu tất cả những quan sát đứng gần nhau, phương sai sẽ nhỏ. Tuy nhiên, việc phân tích và lý giải giá trị phương sai một kiểu trực quan sẽ khó hiểu hơn nhiều so với độ lệch chuẩn chỉnh.
Hạn chế lớn số 1 của việc tận dụng độ lệch chuẩn chỉnh là nó hoàn toàn có thể bị tác động bởi những giá trị ngoại lệ và những giá trị âm.
Duy Sang tổng hợp
Chú thích:[1] Tài liệu ngoại lệ (Outliers) là một điểm tài liệu có sự khác lạ đáng kể so với những quan sát khác. Tài liệu ngoại lệ hoàn toàn có thể xuất hiện do sự thay đổi thang đo hoặc do lỗi từ tài liệu tích lũy (thường thì tài liệu ngoại lệ dạng này sẽ bị loại bỏ khỏi tập tài liệu). Một giá trị ngoại lệ hoàn toàn có thể gây ra vấn đề nghiêm trọng trong quy trình phân tích tài liệu.
–
Tài liệu xem thêm:Carin Viljoen, Linda van der Merwe. (2000). Elementary Statistics (2nd ed.). Pearson South Africa.Illowsky et al. (2013). Introductory Statistics. Houston: OpenStax.Wikipedia. (2021, March 24). Phương sai. Retrieved from Wikipedia: https://vi.wikipedia.org/wiki/Ph%C6%B0%C6%A1ng_sai
–
Những tìm hiểu thêm:
Thống kê mô tả trong nghiên cứu và phân tích – Những đại lượng về trung tâm
Thống kê mô tả trong nghiên cứu và phân tích – Những đại lượng về hình dáng phân phối
Thống kê mô tả trong nghiên cứu và phân tích – Những đại lượng về sự việc tương quan
–
QUÝ ANH/CHỊ CẦN HỖ TRỢ XỬ LÝ, PHÂN TÍCH DỮ LIỆU VUI LÒNG GỬI THÔNG TIN QUA FORM DƯỚI ĐÂY
CHÚNG TÔI SẼ LIÊN HỆ VÀ PHÚC ĐÁP TRONG THỜI GIAN SỚM NHẤT
Đang tải…
